Faszination Goldener Schnitt und Fibonacci-Folge

In der Form von aus Quadraten und Rechtecken zentrisch anwachsenden Spiralen sehen sie sich sehr ähnlich. Der Goldene Schnitt und die Fibonacci-Folge sind gewissermaßen auch verwandt miteinander. Beide spiegeln ein perfektes Teilungsverhältnis und Wachstumsphänomene in der Natur wider.

Der englische Begriff Golden ratio klingt fast wie ein Naturgesetz oder die höchste Vernunft. Und für viele ist es das auch, obwohl ratio hier ein Teilungsverhältnis meint. Viele Wissenschaftler:innen sehen im Goldenen Schnitt aber nur esoterischen Schnickschnack und eine Erfindung der Zeit, als Napoleon und die Europäer sich für das alte Ägypten, die Pyramiden und den Goldenen Schnitt begeisterten. Letzterer sollte plötzlich das Baugerüst des Lebens und für alles Mögliche sein.

Waren die alten Ägypter schon Phi-affin?

In der Cheops-Pyramide will man damals genau diese „sectio aureum“ oder „proportio divina“ erkannt haben, die in der Antike und möglicherweise sogar den alten Ägyptern schon bekannt war. Die Große Pyramide von Gizeh, wie sie auch heißt, war ursprünglich 146,59 m hoch und hatte eine Seitenbreite (ein Basismaß s) von 230,36 m. Dem Satz des Pythagoras zufolge ergibt sich daraus rein rechnerisch eine Seitenhöhe (Länge des Seitendreiecks d) von 186.427 m.

Nimmt man nun diese Seitenhöhe s und teilt sie durch die Hälfte der Basisbreite (1/2 d) erhält man ein Teilungsverhältnis von 1,61857.

Und das kommt dem der Zahl Phi (Φ,  φ oder ϕ) des Goldenen Schnittes von rund 1,61803398874989 schon sehr nahe, so das Argument der Pyramiden- und Phi-Begeisterten im frühen 19. Jahrhundert und bis heute.

So weit so gut, so schön. Aber warum sollte der legendäre Baumeister Hemiunu ausgerechnet die Länge der Seitenhöhe geteilt durch die Hälfte des Basismaßes genommen haben, um auf die Zahl Phi beziehungsweise den Goldenen Schnitt zu kommen? Das erscheint manchen Kritikern der Theorie dann doch etwas arg konstruiert.

Abgesehen davon haben esoterisch Angehauchte um 1800 den Goldenen Schnitt oder die Zahl Φ (Phi) in allem und jedem sehen wollen. Diese Zahl ist zwar so wie π oder die Wurzel aus 2 irrational, lässt sich aber sehr genau berechnen, wie die folgende Formel zeigt:

Die Formel zeigt aber auch, dass die größere Zahl a zur kleineren Zahl b im selben Verhältnis zueinander stehen wie die Summe aus a und b zu a. Das heißt, unabhängig von der Größe der beiden Zahlen ist das Teilungsverhältnis der beiden Zahlen immer dasselbe.

Von Phi zur Goldenen Komposition und Spirale

Die Zahl Φ beziehungsweise der Goldene Schnitt ergibt sich aus dem Teilungsverhältnis von zwei Streckenabschnitten, einem größeren a oder M wie „major“ und einem kleineren b oder m wie „minor“, wobei der größere etwa 61,8 % der Gesamtstrecke einnimmt und der kleinere die verbleibenden rund 38,2 %.

Dieses Teilungs- oder Seitenverhältnis findet sich auch in vielen Bildschirm- und Kinoformaten wieder, beim 16:10-Format etwa oder bei „HD ready“ mit 1.280 × 768 Bildpunkten. Andere Formate wie UHD 4K oder 16 : 9 sind mit einem Seitenverhältnis von 1,77 auch nicht weit von der Zahl Φ, die eben mit 1,6180339887 beginnt.

In der Kunst, in der Fotografie, Architektur und im Design sieht man das Teilungsverhältnis auch als Goldenes Kompositionsraster, wo M als größerer Abschnitt noch einmal in ein M und einem kleineren m unterteilt ist und dieser kleinere Streckenabschnitt rein rechnerisch ungefähr 23,6 % der Gesamtstrecke einnimmt:

Aus der Zweiteilung des Quadraten und des angehängten kleineren Rechtecks lässt sich wie im Goldenen Kompositionsraster auch eine Dreiteilung machen, wie sie unter anderem in der Profi-Fotografie Verwendung findet.  

Diese Zwei- und Dreiteilung entspricht dem Idealbild antiker Skulpturen und Körperproportionen, wonach der Abstand von der Fußsohle zum Bauchnabel etwa 61,8 % der gesamten Körperlänge einnimmt. Der römische Architekt Vitruv, ein Zeitgenosse von Julius Caesar, hatte sein Werk auf diese Ideallinien des menschlichen Körpers aufgebaut. Das hat unter anderem Leonardo da Vinci zur Darstellung des Vitruvianischen Menschen oder Mannes inspiriert.

Oft sieht man die beiden Streckenabschnitte M und m (oder a und b) auch in der Form eines goldenen Rechtecks mit einem seitlichen Quadrat, das etwa 61,8 % der Gesamtlänge hat, und einem kleineren Rechteck, das bei gleicher Höhe rund 38,2 % der Gesamtlänge einnimmt.

Viele Darstellungen zeigen, wie diese Quadrate und Rechtecke im 90-Grad-Winkel um sich herum immer mehr anwachsen und die Quadrate von Kreisbögen angeschnitten sind, die zusammen eine ebenfalls endlos wachsende Spirale ergeben.

Es handelt sich dabei um die sogenannte Goldene Spirale, die nicht nur Esoteriker als Bausteine natürlichen Wachstums sehen. Tatsächlich steckt aber eine andere Spirale dahinter, die der Goldenen Spirale sehr ähnelt, sich aber aus der Fibonacci-Folge von Zahlen ergibt. Bei dieser Zahlenfolge, die mit 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 und 55 beginnt, ist jede Zahl die Summe aus den beiden vorherigen Zahlen.

Schaut man sich die Zahlenfolge genau an, wird man feststellen, dass das Verhältnis zweier benachbarter Fibonacci-Zahlen sich anfangs von Φ (Phi) unterscheidet, dann aber sehr bald zu dieser Zahl des Goldenen Schnitts konvergiert:

1÷1=1
2÷1=2
3÷2=1,5
5÷3=1,6666
8÷5=1,6…
55÷34≈1,617647…

Wie man sieht, kommen die letzten vier Beispiele Teilungsverhältnisse dem des Goldenen Schnittes schon nahe,  987 ÷ 610 (f₁₆ ÷ f₁₅) mit rund 1,6180327 aber noch viel mehr. Und tatsächlich ist die Fibonacci-Folge erst das, was sozusagen den Baumeister natürlichen Wachstums ausmacht. Man kann die Folge unter anderem in Sonnenblumen, Rosenblüten, Schneckenhäusern und sogar in gigantisch großen Gebilden wie Spiralnebeln sehen.

Benannt wurde diese Folge Hunderte Jahre später nach Leonardo da Pisa alias Fibonacci, der sie nach Reisen durch den indo-arabischen Raum in seinem Liber Abaci 1202 verwendete, um damit das theoretische Wachstum einer Kaninchenpopulation zu veranschaulichen. Im selben Buch hat Fibonacci übrigens auch die von ihm novem figurae indorum („neun Ziffern der Inder“) genannten arabischen Zahlen vorgestellt, die damals in Europa noch kaum bekannt waren, aber kurz nach seinem Tod die römischen Zahlen mehr und mehr ablösen sollten.

Die Fibonacci-Folge ist viel älter als der Namensgeber und war im vorchristlichen Indien, möglicherweise sogar schon den alten Babyloniern und Ägyptern bekannt. Und vielleicht war manchen Mathematikern oder Astronomen damals schon bewusst, dass das Verhältnis zweier benachbarter Fibonacci-Zahlen sich sehr schnell der Zahl Φ beziehungsweise dem Goldenen Schnitt nähert.

Wie man Fibonacci-Zahlen errechnen kann

Das hat wohl dazu beigetragen, dass im 18. und 19. unabhängig voneinander zwei französische Mathematiker die nach ihnen benannte Moivre-Binet-Formel oder nur Binet-Formel entwickeln konnten, um die n^te Fibonacci-Zahl zu errechnen. Denn in dieser Formel spielen die Goldene Zahl Φ (Phi) und der negative Kehrwert Ψ (Psi) eine ganz zentrale Rolle. Und obwohl beide Zahlen irrational sind, ergibt sich mit der folgenden Binet-Formel bei ausreichend vielen Nachkommastellen immer ein gerader Wert für die n^te Fibonacci-Zahl:

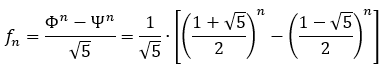
Φ ist dabei wieder die Goldene Zahl Phi, angefangen mit 1,6180339887, und Ψ (oder ψ, Psi) wie der besagte negative Kehrwert von Φ, der mit -0,6180339887 beginnt. Da Null-Kommazahlen bei hohen Potenzen sehr schnell gegen Null gehen, kann man den Ψⁿ-Part in der Binet-Formel bei entsprechend vielen Nachkommastellen von Φ in vielen Fällen auch einfach weglassen:

Wie allerdings leicht festzustellen ist, erhält man mit Φ=1,618033987 bei f₂₀ einen recht passablen Näherungswert von etwa 6765,00002539, bei f₈₀ mit Φ=1,618033987 aber nur eine vage Zahl 23.416.728.290.700.092,32418. Gibt man im Windows-Rechner aber für Φ die Formel „1+5√÷2“ ein, spuckt er potenziert mit 80 geteilt durch die Wurzel aus 5 „brav“ die richtige 80. Fibonacci-Zahl 23.416.728.348.467.685 aus. Wer das überprüfen möchte, kann das über die First 1001 Fibonacci Numbers der Universität von Quebeck in Montreal tun.

Wem es zu mühsam ist, die Binet-Formel zum Errechnen von Fibonacci-Zahlen zu verwenden, kann auch zu einem Trick oder neudeutsch Hack greifen. Denn wenn man 1 durch 89 teilt, erhält man schon die ersten 5 Fibonacci-Zahlen 1, 1, 2, 3, und 5. Teilt man 1 durch 9899, kommt teils von Nullen getrennt eine Kommazahl mit den ersten 10 Fibonacci-Zahlen bis 55 heraus. Fügt man im Nenner vorne und hinten jeweils noch eine 9 hinzu erscheinen, ebenfalls teilweise von Nullen getrennt, die ersten 15 Fibonacci-Zahlen bis 610. Bei 1 geteilt durch 999.998.999.999 erhält man die ersten 29 Fibonacci-Zahlen bis 514.229, bei 1 geteilt durch 99.999.999.989.999.999.999 sogar die ersten 48 Fibonacci-Zahlen, wenn man den Dschungel von Nachkommastellen überhaupt noch durchblicken kann.

Informatik und Bitcoin-Jäger auch Fibonacci-Fieber

Dabei gilt für alle Fibonacci-Zahlen ab der dritten das rekursive Bildungsgesetz:

Wem das alles immer noch nur esoterischer oder schöngeistiger Schnickschnack ist, dem sei gesagt, dass der Goldene Schnitt und die Fibonacci-Folge aufgrund dieses Bildungsgesetzes auch in der Informatik und auf dem Börsenparkett eine Rolle spielen.

Das sogenannte Fibonacci-Retracement (Zurückverfolgung) ist zwar statistisch nicht wirklich nachweisbar, basiert aber auf der Idee, dass die Kapitalmärkte vorangegangenen Auf- und Abwärtsbewegungen folgen. Die als horizontalen Linien gezeichneten Retracement-Levels, auf denen sich die Kurse bewegen, entsprechend dabei üblicherweise denen des Goldenen Schnitts: 23,6%, 38,2%, 50% und 61,8%. Und daran orientieren sich mitunter auch professionelle Bitcoin-Händler, indem sie nahe der Fibonacci Levels 38,2 % und 61,8 % entscheiden, ob es Zeit zum Kaufen oder Verkaufen ist.

In der Informatik findet man die Fibonacci-Folge beziehungsweise ihr rekursives Bildungsgesetz als Fibonacci-Baum und als Fibonacci-Heap. Beide bezeichnen unterschiedliche Datenstrukturen. Letzterer ist mit Heap wie Haufen oder Halde eine Datenstruktur, die als eine Art Vorrangdatenschleife dienen kann. Ein Fibonacci-Baum ist ein Spezialfall des AVL-Baums und binärer Suchbäume. Aber das näher zu erklären, würde hier zu weit führen.

Fazit: Der Goldene Schnitt und die Fibonacci-Folge sind schon faszinierend, auch wenn ihr Wert oft vielleicht nur im Ästhetischen zu finden ist. Die nach Leonardo da Pisa alias Fibonacci benannte Zahlenfolge ist aber gewissermaßen auch Baumeister der Natur und findet in der Informatik und auf dem Börsenparkett sogar praktische Anwendung.

Quelle Titelbild: Pixabay